Diffie-Hellman算法
Deffie-Hellman 算法简介※
Deffie-Hellman(简称 DH) 密钥交换是最早的密钥交换算法之一,它使得通信的双方能在非安全的信道中安全的交换密钥,用于加密后续的通信消息。 Whitfield Diffie 和 Martin Hellman 于 1976 提出该算法,之后被应用于安全领域,比如 Https 协议的 TSL(Transport Layer Security)以 DH 算法作为密钥交换算法。
背景知识※
首先介绍一些跟DH算法相关的数学知识。
离散对数问题※
假设a、p均为素数,则有以下等式:
{ a^1 mod p, a^2 mod p, ..., a^(p-1) mod p } = {1, 2, ... , p-1 } {} 表示集合
对于任意一个数 x,若 0 < x < p,则必定存在唯一的 y 使得 x = a^y mod p,其中 0 < y < p。当p很大时,很难求出y,所以它能做为DH秘钥交换的基础。
求模公式:((a^x mod p)^y) mod p = a^xy mod p※
证明如下:
假设 a^x = mp + n,其中0<n<p,则
C = ((a^x mod p)^y) mod p
= ((mp+n) mod p)^y mod p
= (n mod p)^y mod p
= n^y mod p
= (mp+n)^y mod p
= a^xy mod p三、DH算法原理※
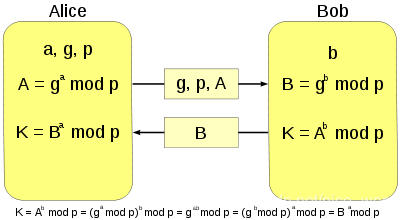
假设Alice和Bob希望在不安全的网络环境中协商一个对称密钥进行通信,那么可按如下步骤进行:
1、首先Alice保存自己的私钥a(随机数),Bob也保存自己的私钥b(随机数)
2、Alice计算 A = g^a mod p,并将g,p,A发给Bob
3、Bob计算 B = g^b mod p,然后将B发给Alice
4、Alice得到对称密钥K = B^a mod p = (g^b mod p)^a mod p = g^ab mod p
5、Bob同样得到对称密钥K = A^b mod p = (g^a mod p)^b mod p = g^ab mod p从此,Alice和Bob得到同样的密钥进行通行。
注意,其中a,b,g^ab mod p, g^ab mod p 是秘密的,其它值均公开。为保证安全性,a,b,p必须是非常大的数字。若p很小(例如p=10),则 g^ab mod p 最多可能有10个值(0~9);若a和b很小,则最多有a*b个值(g^1 mod p,g^2 mod p,… g^ab mod p)。但是g不需要是一个很大的数,通常取2或5。
参考※
1、https://skypacer210.github.io/2014/01/15/little-about-DH/
2、http://wsfdl.com/algorithm/2016/02/04/理解Diffie-Hellman密钥交换算法.html
3、https://zh.wikipedia.org/wiki/迪菲-赫爾曼密鑰交換




